Задача о кубиках. Общий метод решения задач
Задача состоит в выработке плана переупорядочивания кубиков, поставленных друг на друга, как показано на рис. 2.1. На каждом шагу разрешается переставлять только один кубик. Кубик можно взять только тогда, когда его верхняя поверхность свободна. Кубик можно поставить на стол, либо на другой кубик. Для того чтобы построить требуемый план, мы должны отыскать последовательность ходов, реализующую заданную трансформацию.
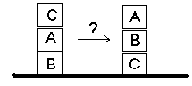 |
Рис. 2.1. Задача перестановки кубиков
Эту задачу можно представлять себе как задачу выбора среди множества возможных альтернатив. В исходной ситуации альтернатива всего одна: поставить кубик C на стол. После того, как кубик C поставлен на стол, мы имеем три альтернативы:
· поставить A на стол или
· поставить A на C, или
· поставить C на A.
Ясно, что альтернативу "поставить C на стол" не имело смысла рассматривать всерьез, так как этот ход никак не влияет на ситуацию.
Как показывает рассмотренный пример, с задачами такого рода связано два типа понятий:
· проблемные ситуации;
· разрешенные ходы или действия, преобразующие одни проблемные ситуации в другие.
Проблемные ситуации вместе с возможными ходами образуют направленный (ориентированный) граф, называемый пространством состояний. Пространство состояний для только что рассмотренного примера дано на рис. 2.2. Вершины графа соответствуют проблемным ситуациям, дуги - разрешенным переходам из одних состояний в другие. Проблема отыскания плана решения задачи эквивалентна проблеме построения пути между заданной начальной ситуацией ("стартовой" вершиной) и некоторой указанной заранее конечной ситуацией, называемой также целевой вершиной.
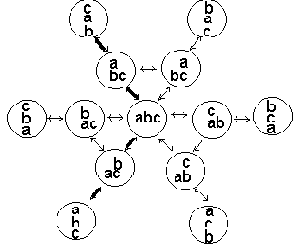 |
Рис. 2.2. Графическое представление задачи манипулирования
кубиками. Выделенный путь является решением задачи
Нетрудно построить аналогичное представление в виде графа и для других популярных головоломок. Наиболее очевидные примеры - это задача о "ханойской башне" и задача о перевозке через реку волка, козы и капусты.
Пространство состояний некоторой задачи определяет "правила игры": вершины пространства состояний соответствуют ситуациям, а дуги - разрешенным ходам или действиям, или шагам решения задачи. Конкретная задача определяется
· пространством состояний,
· стартовой вершиной,
· целевым условием (т. е. условием, к достижению которого следует стремиться); "целевые вершины" - это вершины, удовлетворяющие этим условиям.
Каждому разрешенному ходу или действию можно приписать его стоимость. Например, в задаче манипуляции кубиками стоимости, приписанные тем или иным перемещениям кубиков, будут указывать нам на то, что некоторые кубики перемещать труднее, чем другие. В задаче о коммивояжере ходы соответствуют переездам из города в город. Ясно, что в данном случае стоимость хода - это расстояние между двумя городами.
В тех случаях, когда каждый ход имеет стоимость, мы заинтересованы в отыскании решения минимальной стоимости. Стоимость решения - это сумма стоимостей дуг, из которых состоит "решающий путь" - путь из стартовой вершины в целевую. Даже если стоимости не заданы, все равно может возникнуть оптимизационная задача: нас может интересовать кратчайшее решение.
Прежде чем будут рассмотрены некоторые программы, реализующие классический алгоритм поиска в пространстве состояний, давайте сначала обсудим, как пространство состояний может быть представлено в прологовской программе.
Мы будем представлять пространство состояний при помощи отношения next(X,Y), которое истинно тогда, когда в пространстве состояний существует разрешенный ход из вершины X в вершину Y.
Мы будем говорить, что Y - это преемник вершины X. Если с ходами связаны их стоимости, мы добавим третий аргумент, стоимость хода: next(X,Y,C). Эти отношения можно задавать в программе явным образом при помощи выбора соответствующих фактов. Однако такой принцип оказывается непрактичным и нереальным для тех типичных случаев, когда пространство состояний устроено достаточно сложно. Поэтому отношение следование next обычно определяется неявно, при помощи правил вычисления вершин-преемников некоторой заданной вершины. Другим вопросом, представляющим интерес с самой общей точки зрения, является вопрос о способе представления состояний, т.е. самих вершин. Это представление должно быть компактным, но в то же время оно должно обеспечивать эффективное выполнение необходимых операций, в частности операций вычисления вершин-преемников, а возможно и стоимостей соответствующих ходов.
Рассмотрим в качестве примера задачу манипулирования кубиками. Мы будем рассматривать общий случай, когда имеется произвольное число кубиков, из которых составлены столбики, - один или несколько. Число столбиков мы ограничим некоторым максимальным числом, скажем 3, чтобы задача была интереснее. Такое ограничение, кроме того, является вполне реальным, поскольку рабочее пространство, которым располагает робот, манипулирующий кубиками, ограничено.
Проблемную ситуацию можно представить как список столбиков. Каждый столбик, в свою очередь, представляется списком кубиков, из которых он составлен. Кубики упорядочены в списке таким образом, что самый верхний список находится в голове списка. "Пустые" столбики изображаются как пустые списки. Таким образом, исходную ситуацию можно записать как терм [[c,a,b], [], []]. Целевая ситуация - это любая конфигурация кубиков, содержащая столбик, составленный из всех имеющихся кубиков в указанном порядке. Таких ситуаций три:
[[a,b,c], [], []]
[[], [a,b,c], []]
[[], [], [a,b,c]]
Отношение следование можно запрограммировать, исходя из следующего правила: ситуация S2 есть преемник ситуации S, если в S имеется два столбика C1 и C2, такие, что верхний кубик из C1 можно поставить сверху на C2 и получить тем самым S2.Поскольку все ситуации - это списки столбиков, правило транслируется на Пролог так:
next(S, [C1,[Cub|C2]|T]):- % переставить Cub на столбик C2
select(S,[Cub|C1],S1), % найти первый столбик C1
select(S1,C2,T). % найти второй столбик C2
В нашем примере целевое условие имеет вид:
goal(S):- member([a,b,c],S).
