СТАТИЧЕСКАЯ ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АЦП И ЦАП И ПОГРЕШНОСТИ ПО ПОСТОЯННОМУ ТОКУ
Наиболее важным моментом, характеризующим и ЦАП, и АЦП является тот факт, что их входы или выходы являются цифровыми, а это означает, что сигнал дискретизирован по уровню. То есть N-разрядное слово представляется одним из 2N возможных состояний, поэтому у N-разрядного ЦАП (с фиксированным источником опорного напряжения) может быть только 2N значений аналогового сигнала, а АЦП может выдавать только 2N различных значений двоичного кода. Аналоговые сигналы могут быть при этом представлены в виде напряжений или токов.
Разрешающая способность АЦП или ЦАП может быть выражена несколькими различными способами: весом младшего разряда (LSB), долей от полной шкалы размером в один миллион (ppm FS), милливольтами (мВ) и т.д. Различные устройства (даже от одного производителя) определяются по-разному, так что для успешного сравнения устройств пользователи АЦП и ЦАП должны уметь преобразовывать различные характеристики. Некоторые значения младшего значащего разряда (LSB) приведены в таблице 1.
Таблица 1. Квантование: значение младшего значащего бита(LSB)
| Разреш. способность N | 2N | Напряжение полной шкалы 10В | ppm FS | % FS | dB FS |
| 2-бит | 4 | 2.5 В | 250000 | 25 | -12 |
| 4-бит | 16 | 625 мВ | 62500 | 6.25 | -24 |
| 6-бит | 64 | 156 мВ | 15625 | 1.56 | -36 |
| 8-бит | 256 | 39.1 мВ | 3906 | 0.39 | -48 |
| 10-бит | 1024 | 9.77 мВ (10 мВ) | 977 | 0.098 | -60 |
| 12-бит | 4096 | 2.44 мВ | 244 | 0.024 | -72 |
| 14-бит | 16384 | 610 мкВ | 61 | 0.0061 | -84 |
| 16-бит | 65536 | 153 мкВ | 15 | 0.0015 | -96 |
| 18-бит | 262144 | 38 мкВ | 4 | 0.0004 | -108 |
| 20-бит | 1048576 | 9.54 мкВ (10 мкВ) | 1 | 0.0001 | -120 |
| 22-бит | 4194304 | 2.38 мкВ | 0.24 | 0.000024 | -132 |
| 24-бит | 16777216 | 596 нВ* | 0.06 | 0.000006 | -144 |
*600 нВ - это тепловой шум в полосе частот 10кГц, возникающий на резисторе R=2.2 кОм при 25°C
Легко запомнить: 10-разрядное квантование при значении полной шкалы FS = 10В соответствует LSB = 10 мВ, точность 1000 ppm или 0.1%. Все остальные значения можно вычислить умножением на коэффициенты, равные степени числа 2.
Прежде чем рассматривать различные архитектуры АЦП и ЦАП, необходимо обсудить ожидаемые характеристики и важнейшие параметры цифро-аналоговых и аналого-цифровых преобразователей.
Ниже будет рассмотрено определение погрешностей и технических требований, предъявляемых к АЦП и ЦАП. Это важно для понимания сильных и слабых сторон различных архитектур АЦП и ЦАП.
Первые преобразователи данных применялись в области измерения и управления, где точное значение времени преобразования обычно не имело значения, и скорость передачи данных была невелика. В таких устройствах важны характеристики АЦП и ЦАП по постоянному току, а характеристики, связанные с синхронизацией и характеристики по переменному току не имеют существенного значения. Сегодня ко многим, если не к большинству преобразователей, используемых в системах дискретизации и восстановления сигнала, предъявляются жесткие требования к характеристикам по переменному току (характеристики по постоянному току могут быть не существенны).
На рисунке 1 представлена идеальная функция передачи однополярного 3-разрядного ЦАП, а на рисунке 2 - однополярного 3-разрядного АЦП. В ЦАП входной и выходной сигналы квантованы, и график содержит восемь точек. Независимо от способа аппроксимации этой функции, важно помнить, что реальной характеристикой передачи является не линия, а множество дискретных точек.
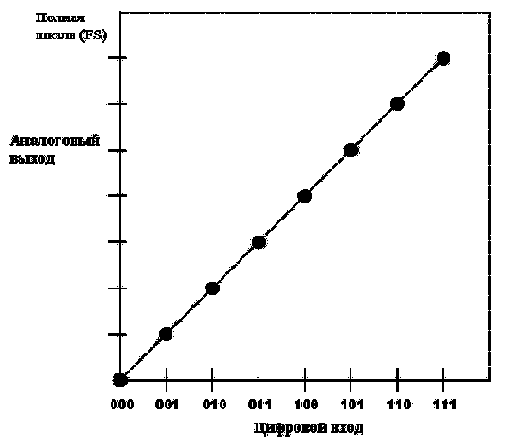
Рисунок 1. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ИДЕАЛЬНОГО 3-РАЗРЯДНОГО ЦАП
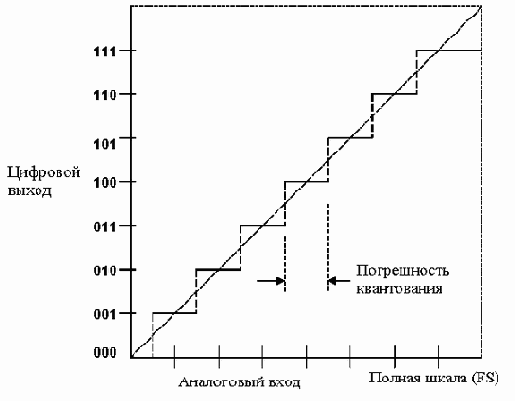
Рисунок 2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ИДЕАЛЬНОГО 3-РАЗРЯДНОГО АЦП
Входной аналоговый сигнал АЦП не квантован, но его выходной сигнал является результатом квантования. Сквозная характеристика АЦП состоит из восьми горизонтальных прямых (при изучении смещения, усиления и линейности АЦП мы будем рассматривать линию, соединяющую средние точки этих отрезков). В любом случае полная цифровая шкала (все "1") соответствует полной аналоговой шкале (опорное напряжение или опорное напряжение умноженное на какой либо коэффициент).
Переходы идеального АЦП к следующему цифровому коду происходят, начиная с напряжения, равного половине младшего разряда до напряжения, меньшего напряжения полной шкалы на половину младшего разряда. Так как аналоговый сигнал на входе АЦП может принимать любое значение, а выходной цифровой сигнал квантуется, может существовать различие до половины младшего разряда между реальным входным аналоговым сигналом и соответствующим ему значением выходного цифрового сигнала.
Этот эффект известен как ошибка (погрешность) или неопределенность квантования и показан на рисунке 2. В устройствах, использующих сигналы переменного тока, эта ошибка квантования приводит к шуму квантования.
В АЦП и ЦАП используются много видов цифровых кодов: двоичные коды, двоичные коды со смещением, коды с дополнением до 1, с дополнением до 2, код Грея, двоично-десятичный код и другие. Здесь нас будут интересовать главным образом проблемы, связанные с аналоговым трактом АЦП и ЦАП. Для иллюстрации этих проблем будет использоваться простой двоичный код или двоичный код со смещением без рассмотрения преимуществ и недостатков этих и любых других способов цифрового кодирования.
В примерах на рисунках 1 и 2 применяются униполярные преобразователи, работающие с сигналом только одной полярности. Это самый простой тип, но в реальных устройствах более полезны биполярные преобразователи. Имеется два типа биполярных преобразователей. Более простой из них - это просто униполярный преобразователь с отрицательным смещением на величину, соответствующую единице старшего разряда (MSB), (во многих преобразователях можно переключать это смещение, чтобы использовать их и как униполярные, и как биполярные). Другой, более сложный тип, известен как знаковый АЦП (sign- magnitude) и имеет кроме N информационных разрядов дополнительный разряд, который показывает знак аналогового сигнала. Знаковые ЦАП применяется довольно редко, на знаковых АЦП сконструированы большинство цифровых вольтметров (DVM).
В АЦП и ЦАП различают четыре типа погрешностей по постоянному току: погрешность смещения, погрешность усиления и два типа погрешностей, связанных с линейностью. Погрешности смещения и усиления АЦП и ЦАП аналогичны погрешностям смещения и усиления в усилителях. На рисунке 3 показано преобразование биполярных входных сигналов (хотя погрешность смещения и погрешность нуля, идентичные в усилителях и униполярных АЦП и ЦАП, различны в биполярных преобразователях, и это следует учитывать). Характеристики передачи и ЦАП, и АЦП могут быть выражены как D=K+GA, где D - цифровой код, А - аналоговый сигнал, K и G - константы.
В униполярном преобразователе K равно 0, в биполярном преобразователе со смещением - 1 старшего значащего разряда. Погрешность смещения - это величина, на которую фактическое значение K отличается от идеального значения. Погрешность усиления - это величина, на которую G отличается от идеального значения. В общем случае, погрешность усиления может быть выражена разностью двух коэффициентов, выраженной в процентах. Эту разность можно рассматривать, как вклад погрешности усиления (в мВ или значениях младшего разряда LSB) в общую погрешность при максимальном значении сигнала. Обычно пользователю предоставляется возможность минимизации этих погрешностей. Обратите внимание, что, в усилителе сначала регулируют смещение при нулевом входном сигнале, а затем настраивают коэффициент усиления при значении входного сигнала, близком к максимальному. Алгоритм настройки биполярных преобразователей более сложен.
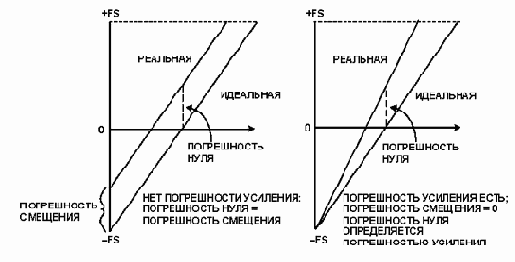
Рисунок 3. ПОГРЕШНОСТЬ СМЕЩЕНИЯ НУЛЯ ПРЕОБРАЗОВАТЕЛЯ И ПОГРЕШНОСТЬ УСИЛЕНИЯ
Интегральная нелинейность ЦАП и АЦП аналогична нелинейности усилителя и определяется как максимальное отклонение фактической характеристики передачи преобразователя от прямой линии. В общем случае, она выражается в процентах от полной шкалы (но может представляться в значениях младших разрядов). Существует два общих метода аппроксимации характеристики передачи: метод конечных точек (end point) и метод наилучшей прямой (best straight line) (см. рисунок 4).
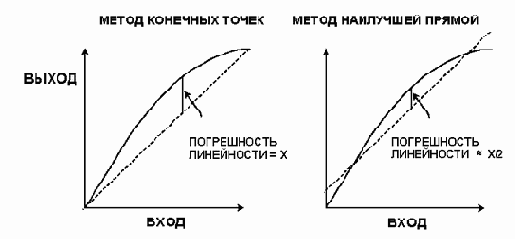
Рисунок 4. МЕТОД ИЗМЕРЕНИЯ СУММАРНОЙ ПОГРЕШНОСТИ ЛИНЕЙНОСТИ
При использовании метода конечных точек измеряется отклонение произвольной точки характеристики (после коррекции усиления) от прямой, проведенной из начала координат. Таким образом в компании Analog Devices, Inc. измеряют значения интегральной нелинейности преобразователей, используемых в задачах измерения и управления (так как величина погрешности зависит от отклонения от идеальной характеристики, а не от произвольного "наилучшего приближения").
Метод наилучшей прямой дает более адекватный прогноз искажений в приложениях, имеющих дело с сигналами переменного тока.
Он менее чувствителен к нелинейностям технических характеристик. По методу наилучшего приближения через характеристику передачи устройства проводят прямую линию, используя стандартные методы интерполяции кривой. После этого максимальное отклонение измеряется от построенной прямой. Как правило, интегральная нелинейность, измеренная таким образом, учитывает только 50% нелинейности, оцененной методом конечных точек. Это делает метод предпочтительным при указании впечатляющих технических характеристик в спецификации, но менее полезным для анализа реальных значений погрешностей. Для приложений, имеющих дело с сигналами переменного тока, лучше определять гармонические искажения, чем нелинейность по постоянному току, так что для определения нелинейности преобразователя необходимость в использовании метода наилучшей прямой возникает довольно редко.
Другой тип нелинейности преобразователей - дифференциальная нелинейность (DNL). Она связана с нелинейностью кодовых переходов преобразователя. В идеальном случае изменение на единицу младшего разряда цифрового кода точно соответствует изменению аналогового сигнала на величину единицы младшего разряда. В ЦАП изменение одного младшего разряда цифрового кода должно вызывать изменение сигнала на аналоговом выходе, в точности соответствующее величине младшего разряда. В то же время в АЦП при переходе с одного цифрового уровня на следующий значение сигнала на аналоговом входе должно измениться точно на величину, соответствующую младшему разряду цифровой шкалы.
Там, где изменение аналогового сигнала, соответствующее изменению единицы младшего разряда цифрового кода, больше или меньше этой величины, говорят об дифференциальной нелинейной (DNL) погрешности. DNL-погрешность преобразователя обычно определяется как максимальное значение дифференциальной нелинейности, выявляемое на любом переходе.
Если дифференциальная нелинейность ЦАП меньше, чем –1 LSB на любом переходе (см. рис.2.12), ЦАП называют немонотонным, и его характеристика передачи содержит один или несколько локальных максимумов или минимумов.
Дифференциальная нелинейность, большая чем + 1 LSB, не вызывает нарушения монотонности, но также нежелательна. Во многих приложениях ЦАП (особенно в системах с обратной связью, где немонотонность может изменить отрицательную обратную связь на положительную) монотонность ЦАП очень важна. Часто монотонность ЦАП явно оговаривается в техническом описании, хотя, если дифференциальная нелинейность гарантированно меньше единицы младшего разряда (то есть, |DNL| . 1LSB), устройство будет обладать монотонностью, даже если это явно не указывается.
Бывает, что АЦП немонотонен, но наиболее распространенным проявлением DNL в АЦП являются пропущенные коды. (см. рис.2.13). Пропущенные коды (или немонотонность) в АЦП столь же нежелательны, как немонотонность в ЦАП. Опять таки, это возникает при DNL > 1 LSB.
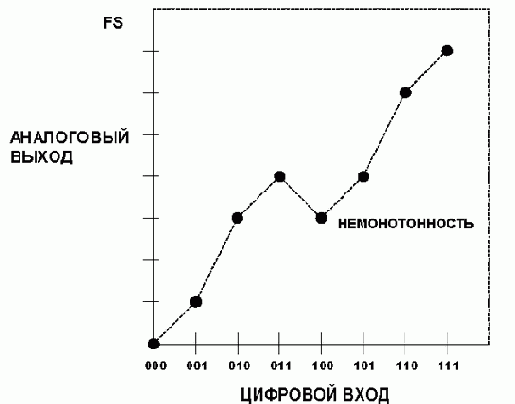
Рис. 2.12 Функция передачи неидеального 3-разрядного ЦАП
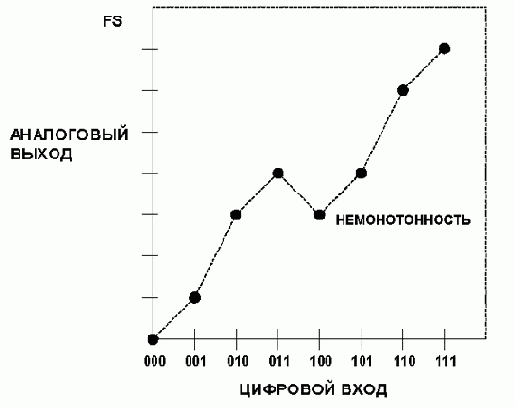
Рис. 2.13 Функция передачи неидеального 3-разрядного ЦАП
Определение отсутствующих кодов сложнее, чем определение немонотонности. Все АЦП характеризуются некоторым шумом перехода (transition noise), иллюстрируемым на рис.2.14 (представьте себе этот шум как мелькание последней цифры цифрового вольтметра между соседними значениями). По мере роста разрешающей способности диапазон входного сигнала, соответствующий уровню шума перехода, может достичь или даже превысить значение сигнала, соответствующее единице младшего разряда. В таком случае, особенно в сочетании с отрицательной DNL- погрешностью, может случиться так, что появятся некоторые (или даже все) коды, где шум перехода будет присутствовать во всем диапазоне значений входных сигналов. Таким образом, возможно существование некоторых кодов, для которых не существует значения входного сигнала, при котором этот код гарантированно бы появился на выходе, хотя и может существовать некоторый диапазон входного сигнала, при котором иногда будет появляться этот код.
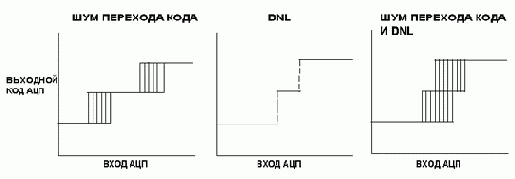
Рис. 2.14 Совместное действие шумов перехода кода и дифференциальной нелинейности (DNL)
Для АЦП с невысокой разрешающей способностью можно определить условие отсутствия пропущенных кодов как сочетание шума перехода и дифференциальной нелинейности, при котором гарантировался бы некоторый уровень (скажем, 0.2 LSB) свободного от шума кода для всех кодов.Однако при этом невозможно достичь столь высокой разрешающей способности, которую обеспечивают современные сигма-дельта АЦП, или даже меньшей разрешающей способности для АЦП с широкой полосой пропускания. В этих случаях производитель должен определять уровни шумов и разрешающую способность каким-нибудь другим способом. Не так важно, какой метод используется, но спецификация должна содержать четкое определение используемого метода и ожидаемые характеристики.
