Искажения и шум в идеальном N-разрядном АЦП

До сих пор мы анализировали процесс дискретизации без рассмотрения такой операции АЦП, как квантование. Теперь будем трактовать АЦП как идеальный дискретизатор, но учитывать при этом эффекты квантования.

Идеальный N-разрядный АЦП имеет погрешности (по постоянному или переменному току), связанные только с процессами дискретизации и квантования. Максимальная погрешность, которую имеет идеальный АЦП при оцифровывании входного сигнала, равна ±1/2 LSB. Любой аналоговый сигнал, поступающий на вход идеального N- разрядного АЦП, производит шум квантования. Среднеквадратичное значение шума (измеренное по ширине полосы Найквиста, от постоянного тока до fs/2) приблизительно равно весу наименьшего значащего разряда (LSB) q, деленному на v12. (см. Приложение 2). При этом предполагается, что амплитуда сигнала составляет, по крайней мере, несколько младших разрядов, так что выход АЦП изменяет свое состояние почти при каждом отсчете. Сигнал ошибки квантования от входного линейного пилообразного сигнала аппроксимируется сигналом пилообразной формы с максимальным размахом q, и его среднеквадратичное значение равно q/v12 (см. рис.2.15).

Можно показать, что отношение среднеквадратичного значения синусоидального сигнала, соответствующего полной шкале, к среднеквадратичному значению шума квантования (выраженное в дБ) равно:

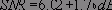
где N - число разрядов в идеальном АЦП. Это уравнение имеет силу только в том случае, если шум измерен на полной ширине полосы Найквиста от 0 до fs /2, как показано на рис.2.16. Если ширина полосы сигнала BW меньше fs /2, то значение отношения сигнал/шум (SNR) в пределах ширины полосы сигнала BW возрастет вследствие уменьшения энергии шума квантования в пределах ширины полосы. Для этого условия правильным будет следующее выражение:

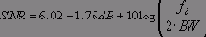
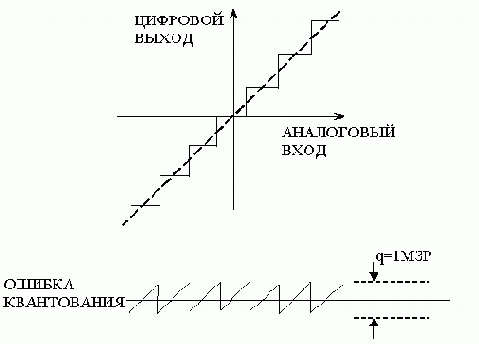
Рис. 2.15 Шум квантования идеального N-разрядного АЦП

Рис. 2.16 Спектр шума квантования

Приведенное уравнение отражает состояние, именуемое избыточной дискретизацией, при котором частота дискретизации выше, удвоенной ширины полосы сигнала.
Корректирующую величину часто называют запасом по дискретизации. Обратите внимание, что для заданной ширины полосы сигнала удвоение частоты дискретизации увеличивает отношение сигнал/шум на 3 дБ.

Хотя среднеквадратичное значение шума точно описывается формулой

, его частотное распределение может сильно зависеть от входного аналогового сигнала. Например, корреляция будет больше для периодического сигнала малой амплитуды, чем для случайного сигнала большой амплитуды. Весьма часто в теории полагают, что шум квантования проявляется в виде белого шума, распределенного равномерно по всей ширине полосы Найквиста от 0 до fд /2. К сожалению, это не так. В случае сильной корреляции шум квантования будет сконцентрирован около каких угодно гармоник входного сигнала, но только не там, где бы Вы хотели.

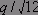
В большинстве устройств входной сигнал АЦП (он обычно смешан с некоторым шумом) представляет собой полосу частот со случайным шумом квантования. Тем не менее, в устройствах спектрального анализа (или при выполнении БПФ на АЦП, использующих спектрально чистый синусоидальный сигнал, см. рис.2.17) корреляция между шумом квантования и сигналом зависит от отношения частоты дискретизации к частоте входного сигнала. Это демонстрируется на рис.2.18, где идеальный выход 12-разрядного АЦП представлен с использованием БПФ с 4096 точками. На левом графике отношение частоты дискретизации к входной частоте было выбрано равным точно 32, и худшая гармоника составляет 76 дБ от основной частоты. Правый график показывает эффект некоторого смещенного отношения, приводящего к относительному разбросу спектра случайного шума, благодаря которому динамический диапазон, свободный от гармоник (SFDR), достигает 92 дБ. В обоих случаях среднеквадратичное значение всех шумовых компонентов равно q/v12, но в первом случае шум сконцентрирован около гармоник основной частоты.

Рис. 2.17 Анализ динамических характеристик идеального N-разрядного АЦП

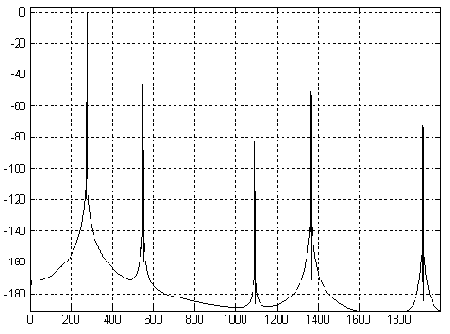
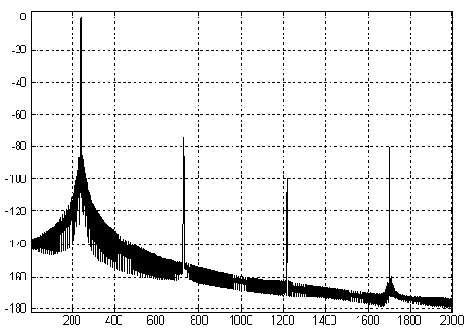
Рис. 2.18 Влияние отношения частоты дискретизации к входной частоте на динамический диапазон (SFDR) для идеального АЦП

Обратите внимание, что это изменение нелинейных искажений АЦП является следствием процесса дискретизации и корреляции ошибки квантования с входной частотой. В практике аналого-цифрового преобразования ошибка квантования вообще проявляется как случайный шум из-за случайной природы широкополосного входного сигнала и того факта, что обычно имеется небольшой шум системы, который действует, как подмешиваемый псевдослучайный сигнал при дальнейшем распределении спектра ошибки квантования.

Отмеченное очень важно, потому что для определения характеристик АЦП часто используется быстрое преобразование Фурье (БПФ) для монотонного синусоидального сигнала. Для точного измерения нелинейных искажений АЦП должны быть предприняты шаги, гарантирующие, что испытательная установка верно измеряет искажения, идущие от АЦП, с учетом эффекта корреляции шума квантования. Это достигается соответствующим выбором соотношения испытательных частот и частот дискретизации, а иногда – добавлением к входному сигналу некоторого шума (псевдослучайного сигнала).

Вернувшись к рис.2.18, обратите внимание, что минимальный уровень шума, полученного с помощью БПФ, приблизительно равен 100 дБ от полной шкалы АЦП, тогда как т еоретическое отношение сигнал/шум 12-разрядного АЦП равно 74 дБ. Минимальный уровень шума от БПФ не равен отношению сигнал/шум АЦП, потому что БПФ действует, подобно аналоговому анализатору спектра с шириной полосы fs /M, где М – число точек БПФ. Теоретически минимальный уровень шума БПФ равен 10 log10 (M/2) дБ, то есть ниже минимального уровня шума квантования из-за так называемого выигрыша БПФ в отношении сигнал/шум (см. рис.2.19). В случае идеального 12-разрядного АЦП с отношением сигнал/шум 74 дБ, использование БПФ с 4096 точками привело бы к выигрышу в отношении сигнал/шум в 10 log10 (4096/2) = 33 дБ, приводя, таким образом, к предельному отношению сигнал/шум 74+33=107 дБ. В действительности, минимальный уровень шума БПФ может быть еще уменьшен за счет увеличения количества точек БПФ, подобно тому, как минимальный уровень шума аналогового анализатора спектра может быть уменьшен за счет сужения ширины полосы пропускания.

При испытаниях АЦП, использующих БПФ, важно быть уверенным, что количество точек БПФ достаточно велико для того, чтобы нелинейные искажения можно было отличить от минимального уровня ума БПФ.

Рис. 2.19 Уровень шума идеального 12-разрядного АЦП при 4096-точечном БПФ

Искажение и шум в реальных АЦП

На практике дискретизация сигнала в АЦП (с интегрированным устройством выборки- хранения УВХ), независимо от архитектуры, проходит при наличии шумов и искажений сигнала, как это показано на рис.2.20. Широкополосному аналоговому входному буферу присущи широкополосный шум, нелинейность и конечная ширина полосы. УВХ (SHA) вносит дальнейшую нелинейность, ограничение полосы и дрожание апертуры. Квантующая часть АЦП вносит шум квантования, интегральную и дифференциальную нелинейности. В этом обсуждении предполагается, что сигналы с последовательных выходов АЦП загружаются в буферную память длиной М и что БПФ процессор имеет спектральный выход. Также допускается, что арифметические операции БПФ не вносят никаких существенных погрешностей в АЦП. Однако при проверке минимального выходного уровня шума должен быть рассмотрен выигрыш в отношении сигнал/шум БПФ (зависящий от M).

МОДЕЛЬ АЦП, ПОКАЗЫВАЮЩАЯ ИСТОЧНИКИ

ШУМОВ И ИСКАЖЕНИЙ СИГНАЛА

Рис. 2.20

Приведенный ко входу тепловой шум

Широкополосные внутренние цепи АЦП вносят некоторое среднеквадратичное значение широкополосного шума из-за воздействия тепла и дисперсии шума kT/C. Этот шум присутствует даже для сигналов постоянного тока и объясняет тот факт, что результатом работы большинства широкополосных (с высокой разрешающей способностью) АЦП является распределение кодов, сконцентрированное вокруг номинального значения входного сигнала (см. рис.2.21). Чтобы измерить его значение, вход АЦП заземляется, накапливается большое количество выходных отсчетов и составляется график в виде гистограммы (иногда упоминаемый как гистограмма с заземленным входом). Так как шум имеет почти Гауссово распределение, стандартное отклонение гистограммы легко рассчитывается (см.

Приложение 3) в соответствии с эффективным среднеквадратичным значением входного шума. Обычной практикой для выражения среднеквадратичного значения шума является его выражение в терминах младших разрядов, хотя оно может быть выражено как среднеквадратичное значение напряжения.

Существуют различные способы описания характеристик аналогового тракта АЦП. На ранней стадии технологии АЦП (более 30 лет назад) не существовало серьезной стандартизации характеристик аналогового тракта, измерительного оборудования и методов или они не были хорошо изучены либо были недоступны. Спустя почти 30 лет производители и заказчики узнали больше об измерении динамических характеристик преобразователей. Спецификации наиболее популярных сегодня преобразователей представлены на рис.2.22. Фактически все спецификации представляют характеристики преобразователя в частотной области. БПФ является основой практически всех измерений и подробно обсуждается в разделе 5 этой книги.

ГИСТОГРАММА, ПОКАЗЫВАЮЩАЯ РАСПРЕДЕЛЕНИЕ

ВЕРОЯТНОСТИ ВЫХОДНОГО КОДА

ПРИ ДЕЙСТВИИ ШУМА НА ВХОД АЦП

Рис. 2.21

Гармонические искажения

Наихудшие гармоники

Общие гармонические искажения (THD)

Общие гармонические искажения и шум (THD + N)

Отношение сигнал-шум и искажения (SINAD, or S/N +D)

Эффективное количество разрядов (ENOB)

Отношение сигнал-шум (SNR)

Аналоговая полоса пропускания (для полного сигнала, для малого сигнала)

Динамический диапазон, свободный от гармоник (SFDR)

Двухтональные интермодуляционные искажения

Многотональные интермодуляционные искажения

ОПРЕДЕЛЯЮЩИЕ ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ

АЦП

Рис. 2.22

Явления интегральных и дифференциальных нелинейных искажений

Одним из важнейших для понимания аспектов при определении нелинейности АЦП и ЦАП является то, что передаточная функция преобразователя данных имеет особенности, которые отсутствуют в обычных линейных устройствах типа операционных усилителей (ОУ) или усилительных блоков. Полная интегральная нелинейность АЦП обусловлена интегральной нелинейностью входного буфера, УВХ (SHA) и полной интегральной нелинейностью передаточной функции АЦП.

Но дифференциальная нелинейность, которая присутствует исключительно вследствие цифрового кодирования, может значительно изменяться в зависимости от принципов применяемого цифрового кодирования АЦП. Полная интегральная нелинейность дает составляющие искажений, у которых амплитуда изменяется в зависимости от амплитуды входного сигнала. В частности, интермодуляционные составляющие второго порядка увеличиваются на 2 дБ при увеличении сигала на 1 дБ, а составляющие третьего порядка увеличиваются на 3 дБ при повышении уровня сигнала на 1 дБ.

Дифференциальная нелинейность в передаточной функции АЦП порождает гармоники, которые зависят не только от амплитуды сигнала, но и от положения точки дифференциальной нелинейности на передаточной функции АЦП. На рис.2.23 показаны две передаточные функции АЦП, имеющих различную дифференциальную нелинейность. Левая диаграмма показывает погрешность, которая имеет место при наличии нелинейности в середине шкалы. Поэтому сигнал, проходящий через эту точку, и при "больших", и при "малых" сигналах подвергается искажениям, не зависящим от относительной амплитуды сигнала. Правая диаграмма показывает другую передаточную функцию АЦП, которая имеет погрешности дифференциальной нелинейности в точках, соответствующих 1/4 и 3/4 полной шкалы. Сигналы, превышающие 1/2 шкалы АЦП, подвергнутся действию этих искажений, в то время как сигналы, не превышающие 1/2 шкалы размаха, не имеют искажений.

ТИПИЧНЫЙ ВИД ДИФФЕРЕНЦИАЛЬНОЙ

НЕЛИНЕЙНОСТИ (DNL) АЦП/ЦАП

Рис. 2.23

Большинство быстродействующих АЦП разработаны так, чтобы дифференциальная нелинейность равномерно распределялась по всей ширине динамического диапазона АЦП. Поэтому для сигналов, которые находятся в пределах нескольких дБ полной шкалы АЦП, полная интегральная нелинейность передаточной функции определяет гармонические искажения. Для сигналов более низких уровней содержание гармоник определяется дифференциальной нелинейностью и в общем случае не уменьшается с уменьшением амплитуды сигнала.

Нелинейные искажения, наихудшая гармоника, общие нелинейные искажения (THD), общие нелинейные искажения плюс шум (THD + N)

Существует множество способов количественного описания искажений в АЦП. Анализ БПФ может использоваться для измерения амплитуды различных гармоник сигнала. Гармоники входного сигнала могут отличаться от других составляющих искажений их положением в частотном спектре. На рис.2.24 показан 7 МГц входной сигнал, дискретизированный с частотой 20 MSPS, и положение его первых девяти гармоник. Гармоники частоты fa попадают на частоты, равные |±Kfs±nfa|, где n – порядок гармоники и K = 0, 1, 2, 3, .... В общем, только вторая и третья гармоники точно определены в технической документации, потому что они, как правило, наибольшие, хотя в некоторых случаях могут определять значение наихудшей гармоники (worst harmonic). Нелинейные искажения обычно определяются в дБс (децибелы ниже несущей), хотя на звуковых частотах они могут быть определены в процентах. Нелинейные искажения, как правило, определяются при входным сигнале с размахом, близким к полной шкале преобразователя (от 0,5 до 1 дБ ниже полной шкалы для предотвращения амплитудного ограничения), хотя возможно определение их и на любом другом уровне. Для сигналов с размахом, существенно меньшим полной шкалы, из-за дифференциальной нелинейности преобразователя другие составляющие (не прямые гармоники) могут ухудшать характеристики прибора.

РАСПОЛОЖЕНИЕ СОСТАВЛЯЮЩИХ ГАРМОНИЧЕСКИХ

ИСКАЖЕНИЙ: ВХОДНОЙ СИГНАЛ = 7 МГЦ,

СКОРОСТЬ (ЧАСТОТА) ДИСКРЕТИЗАЦИИ = 20 MSPS

Рис. 2.24

Величина полных нелинейных искажений (THD) определяется как отношение среднеквадратичного значения основной частоты сигнала к среднему значению корня из суммы квадратов (root-sum-square) его гармоник (существенны только первые пять). Полные нелинейные искажения АЦП также определяются входным сигналом величиной, близкой к полной шкале АЦП, но могут быть найдены и на любом ином уровне. Полные нелинейные искажения плюс шум (THD + N) являются отношением среднеквадратичного значения основной частоты сигнала к среднему значению корня из суммы квадратов (root-sum-square) его гармоник и всех шумовых компонент (исключая постоянную составляющую).

Ширина полосы, в которой измеряется шум, должна быть задана. В случае БПФ ширина полосы занимает промежуток от 0 до fs/2 (если ширина полосы измерения от 0 до fs/2, THD+N = SINAD – см. ниже).

Показатель сигнал/шум/искажения (SINAD), показатель сигнал/шум (SNR) и эффективное число разрядов (ENOB)

Показатель сигнал/шум/искажения (SINAD) и показатель сигнал/шум (SNR) заслуживают особого внимания, потому что все еще имеются некоторые разногласия между производителями АЦП относительно их точного определения. Сигнал/шум/искажения (SINAD, или S/N+D) – это отношение среднеквадратичного значения амплитуды сигнала к среднему значению корня из суммы квадратов (RSS) всех других спектральных компонентов, включая гармоники, но исключая постоянную составляющую. SINAD является хорошим индикатором общих динамических характеристик АЦП, таких как функция входной частоты, потому что включает все компоненты, которые создают шум (включая тепловой шум) и искажения. Он часто представляется в виде графика для различных амплитуд входного сигнала. Если ширина полосы сигнала и шума одинаковы, то SINAD = THD+N. Типичный график для 12-разрядного АЦП AD9220 с частотой дискретизации 10 MSPS представлен на рис.2.26.

ОТНОШЕНИЕ СИГНАЛ/(ШУМ И ИСКАЖЕНИЯ) (SINAD),

ЭФФЕКТИВНАЯ РАЗРЯДНОСТЬ (ENOB),

ОТНОШЕНИЕ СИГНАЛ/ШУМ (SNR)

Рис. 2.25

SINAD (Отношение сигнала к шуму и искажениям):
Отношение среднеквадратичного значения амплитуды сигнала

к среднему значению корня из суммы квадратов (RSS) всех

остальных составляющих спектра, включая гармоники, но

исключая постоянную составляющую.

ENOB (Эффективная разрядность):

ENOB =

SNR (Отношение сигнал/шум или отношение сигнал/шум без

гармоник):

Отношение среднеквадратичного значения амплитуды сигнала

к среднему значению корня из суммы квадратов (RSS) всех

остальных составляющих спектра, исключая первые пять

гармоник и постоянную составляющую

SINAD – 1.76 дБ

6.02 дБ

ОТНОШЕНИЕ СИГНАЛ/(ШУМ И ИСКАЖЕНИЯ) (SINAD) И ЭФФЕКТИВНОЕ ЧИСЛО РАЗРЯДОВ (ENOB) ПРИ РАЗЛИЧНЫХ УРОВНЯХ ВХОДНОГО СИГНАЛА 12-РАЗРЯДНОГО, 10 MSPS АЦП AD9220

ЧАСТОТА АНАЛОГОВОГО СИГНАЛА НА ВХОДЕ (МГц)

Рис. 2.26

График SINAD показывает, где характеристики АЦП по переменному току ухудшаются из-за искажений на высоких частотах, причем обычно этот график строится для частот, значительно превышающих частоту Найквиста для оценки характеристик в приложениях, использующих субдискретизацию. SINAD часто преобразуется в эффективное число разрядов (ENOB), используя выражение для теоретического отношения сигнал/шум идеального N-разрядного АЦП: SNR = 6,02N + 1,76dB. Уравнение решается для N, и значение отношения сигнал/шум заменяется на SINAD:

Отношение сигнал/шум (SNR или SNR без гармоник) рассчитывается так же, как и SINAD, за исключением того, что из выражения исключаются гармоники сигнала и оставлены только шумовые составляющие. Практически, необходимо исключить только первые пять доминирующих гармоник. Показатель сигнал/шум будет ухудшаться на высоких частотах, но не так быстро как SINAD, так как из него исключены компоненты гармоник.

Во многих описаниях АЦП довольно свободно принимается, что SINAD равно SNR, так что инженер должен быть внимательным при интерпретации этих характеристик.

Аналоговая ширина полосы

Аналоговая ширина полосы АЦП – это та частота, на которой спектральный выход основной смещенной частоты (как было определено при анализе БПФ) уменьшается на 3 дБ. Она может быть определено как для малого сигнала (полоса пропускания малого сигнала SSBW), так и для сигнала на уровне полной шкалы (полоса пропускания максимального сигнала FPBW). Поэтому между производителями могут встречаться большие различия в характеристиках.

Как и для усилителя, спецификация аналоговой полосы пропускания преобразователя не предполагает, что АЦП поддерживает хорошие характеристики гармонических искажений во всей полосе частот. В действительности, SINAD (или ENOB) большинства АЦП начинает ухудшаться значительно раньше, чем частота входного сигнала приблизится к значению, соответствующему ослаблению на 3 дБ. На рис.2.27 представлены эффективное число разрядов (ENOB) и частотная характеристика входного сигнала, соответствующего полной шкале АЦП с FPBW 1 МГц, но ENOB начинает быстро понижаться на частотах, превышающих 100 кГц.

ЗАВИСИМОСТЬ УСИЛЕНИЯ (ПОЛОСА ПРОПУСКАНИЯ) АЦП И ЭФФЕКТИВНОЙ РАЗРЯДНОСТИ (ENOB) ОТ ЧАСТОТЫ СИГНАЛА ПОКАЗАНЫ ВАЖНЫЕ ПАРАМЕТРЫ СПЕЦИФИКАЦИИ ENOB

Рис. 2.27

Динамический диапазон, свободный от гармоник(SFDR)

Вероятно, наиболее значительным моментом для АЦП, используемых в коммуникационных приложениях, является их динамический диапазон, свободный от гармоник (SFDR). Спецификация SFDR для АЦП аналогична спецификации точки пересечения уравнений третьего порядка для смесителей и малошумящих усилителей (LNA). SFDR АЦП определяется как отношение среднеквадратичного значения амплитуды сигнала к среднеквадратичному значению пикового побочного спектрального состава, измеренного в первой зоне Найквиста от 0 до fs/2. На графике SFDR строится как функция амплитуды сигнала и может быть выражен относительно амплитуды сигнала (дБс) или полной шкалы АЦП (dBFS), как показано на рис.2.28.

СВОБОДНЫЙ ОТ ГАРМОНИК ДИНАМИЧЕСКИЙ

ДИАПАЗОН (SFDR)

Рис. 2.28

Для сигнала, имеющего амплитуду, близкую к полной шкале АЦП, пиковая спектральная линия определяется несколькими первыми гармониками основной частоты. Но когда сигнал опускается на несколько дБ ниже полной шкалы, появляются другие спектральные линии, которые не являются прямыми гармониками входного сигнала. Это, как обсуждалось ранее, происходит из-за дифференциальной нелинейности передаточной функции АЦП. Поэтому, SFDR учитывает все источники искажения, независимо от их происхождения.

Широкополосный 12-разрядный АЦП AD9042 с частотой дискретизации 41 MSPS, является АЦП, разработанным для коммуникационных приложений, где SFDR очень важен. На рис.2.29 представлены характеристики SFDR для входного сигнала 19,5 МГц, дискретизированного с частотой 41 MSPS. Обратите внимание, что минимум SFDR в 80 дБс получен во всей первой зоне Найквиста (от 0 до 20 МГц). На графике также показано значение SFDR, выраженное как dBFS.

В общем случае SFDR существенно больше, чем теоретическое значение отношения сигнал/шум N-разрядного АЦП (6,02N + 1,76 дБ).

Например, 12-разрядный АЦП AD9042 с SFDR 80 дБс имеет типичное отношение сигнал/шум 65 дБс (теоретическое 74 дБ). Это объясняется тем, что есть существенное различие между измерениями искажений и шума. Выигрыш в отношении сигнал/шум БПФ (33 дБ для БПФ с 4096 точками) допускает существование частотных линий значительно ниже наблюдаемого минимального уровня шума. Увеличение разрешающей способности АЦП может увеличивать отношение сигнал/шум АЦП, но не обязательно улучшает его SFDR.

ЗАВИСИМОСТЬ SFDR ОТ ВХОДНОЙ МОЩНОСТИ ДЛЯ 12-РАЗРЯДНОГО 41 MSPS АЦП AD9042

Рис. 2.29

Двухтональные интермодуляционные искажения (IMD)

Двухтональные интермодуляционные искажения (IMD) измеряют, подавая на АЦП два спектрально чистых синусоидальных сигнала с частотами f1 и f2, обычно довольно близкими друг к другу. Амплитуда каждой компоненты устанавливается на 6 дБ ниже полной шкалы для того, чтобы АЦП не входил в ограничение при совпадении сигналов по фазе. На рис.2.30 показано местоположение составляющих второго и третьего порядка. Обратите внимание, что составляющие второго порядка приходятся на те частоты, которые могут быть удалены цифровыми фильтрами. Но составляющие третьего порядка 2f2–f1 и 2f1–f2 располагаются близко к исходным сигналам и их более трудно фильтровать. Если не определено иное, двухтональные интермодуляционные искажения (IMD) относятся к этим составляющим третьего порядка. Значение интермодуляционных искажений выражается в дБс относительно уровня любой из двух первоначальных частот, а не их суммы.

Обратите внимание, что, если частоты имеют значения, близкие к fs/4, то третьи гармоники основных частот могут затруднить идентификацию компонент 2f2–f1 и 2f1–f2. Это происходит потому, что третья гармоника fs/4 равна 3 fs/4 и она, соответственно, порождает компоненту fs – 3 fs/4 = fs/4. Точно также, если две частоты располагаются близко к fs/3, то вторая гармоника может мешать измерениям по той же причине: вторая гармоника fs/3 равна 2 fs/3 и она, соответственно, порождает компоненту fs – 2 fs/3 = fs/3.

СОСТАВЛЯЮЩИЕ 2-ГО И 3-ГО ПОРЯДКА В РЕЗУЛЬТАТЕ ВОЗДЕЙСТВИЯ ДВУХТОНАЛЬНОГО СИГНАЛА f 1 = 5 МГц, f 2 = 6 МГц

Рис. 2.30

Концепция точек пересечения кривых второго и третьего порядка неправильна для АЦП, потому что уровень составляющих искажений изменяется непредсказуемым образом (он не является функцией амплитуды сигнала). АЦП начинает ограничивать сигналы, приближающиеся к полной шкале, не постепенно (точка ограничения на 1 дБ отсутствует). Как только сигнал превышает диапазон изменения входных сигналов АЦП, АЦП действует в качестве жесткого ограничителя, внезапно создавая критические искажения из-за амплитудного ограничения. С другой стороны, для сигналов, значительно меньших полной шкалы, уровень искажений остается относительно постоянным и не зависимым от уровня сигнала.

В коммуникационных приложениях часто измеряется многотональный SFDR. Большим числом тонов более точно моделируется широкополосный частотный спектр систем сотовой телефонии типа AMPS и GSM. На рис.2.31 представлены характеристики 4-тональной интермодуляции 12-разрядного АЦП AD6640 с быстродействием 65 MSPS. Большое значение SFDR увеличивает способность приемника фиксировать слабые сигналы в присутствии сильных и предотвращать маскировку слабых сигналов интермодуляционными помехами сильных.

ТЕСТИРОВАНИЕ МНОГОТОНАЛЬНЫМ СИГНАЛОМ: 12-РАЗРЯДНЫЙ 65 MSPS АЦП AD6640

Рис. 2.31

Уровень собственных шумов (NPR)

П роверка уровня собственных шумов широко применяется для измерения характеристики передачи линии связи, использующей систему с многоканальным доступом с частотным разделением каналов (FDMA) (см. Приложение 4). В типичной FDMA-системе звуковые каналы шириной 4 кГц загружаются в "частотный стек" для передачи через коаксиальный кабель, радиорелейную станцию микроволнового диапазона или спутниковое оборудование. На приемном конце системы FDMA данные демультиплексируются и возвращаются к 4 кГц индивидуальным каналам основной полосы частот. В FDMA системе, имеющей более 100 каналов, сигнал FDMA может быть аппроксимирован Гауссовым шумом с соответствующей шириной полосы.

Индивидуальный 4 кГц канал может быть проверен на предмет собственных шумов, используя узкополосный режекторный фильтр и специально настроенный приемник, который измеряет мощность шума внутри 4 кГц полосы подавления (см. рис.2.32).

Измерения уровня собственных шумов (NPR) производятся весьма просто. Среднеквадратичное значение мощности шума сигнала внутри полосы подавления измеряется узкополосным приемником при отключенном режекторном фильтре. Затем подключается режекторный фильтр и измеряется остаточный шум внутри канала. Отношение этих двух значений, выраженное в дБ, является уровнем собственных шумов (NPR). Для соответствующей характеристики системы проверяется несколько интервалов частот в пределах шумовой полосы (в области низких, средних и высоких частот). Измерение уровня собственных шумов в АЦП осуществляется подобным же образом, за исключением использования аналогового приемника, который заменен буферной памятью и процессором БПФ.

ИЗМЕРЕНИЕ УРОВНЯ СОБСТВЕННЫХ ШУМОВ (NPR)

Рис. 2.32

Обычно уровень собственных шумов (NPR) представляется на графике. График NPR отображает функцию среднеквадратичного значения уровня шума в пиковом диапазоне системы. Для очень низкого уровня широкополосного сигнала нежелательным (в нецифровых системах) является, прежде всего, тепловой шум, который независим от уровня входного широкополосного сигнала. В этой части кривой увеличение на 1 дБ подаваемого широкополосного входного сигнала вызывает увеличение уровня собственных шумов на 1 дБ. По мере увеличения уровня широкополосного входного сигнала, усилители в системе начинают работать с перегрузкой, создавая интермодуляционные помехи, которые увеличивают уровень шума системы. По мере того, как входной сигнал продолжает увеличиваться, усиливаются эффекты "шумовой перегрузки" и NPR существенно уменьшается. FDMA-системы обычно работают в режиме, когда уровень подаваемого широкополосного сигнала на несколько дБ ниже точки максимума уровня собственных шумов.

В цифровой системе с АЦП шум в пределах интервала является, прежде всего, шумом квантования, если используются низкие уровни входного широкополосного сигнала.

В этой части кривая NPR имеет линейную зависимость. По мере того, как уровень широкополосного входного сигнала увеличивается, некоторое время сохраняется линейное соответствие между уровнем входного шума и NPR. Но на некотором уровне шум амплитудного ограничения, вызванный жестким ограничивающим действием АЦП, начинает преобладать. Теоретическая кривая для 10-, 11- и 12-разрядных АЦП представлена на рис.2.33 (см. Приложение 5).

В многоканальных высокочастотных коммуникационных системах NPR может, также, использоваться для моделирования искажений, вызванных большим количеством индивидуальных каналов, подобно тому, как это имеет место в FDMA-системе. При этом режекторный фильтр помещается между источником шума и АЦП, и результат расчета БПФ используется вместо аналогового приемника. Для AD9042 ширина полосы режекторного фильтра устанавливается в несколько мегагерц, как показано на рис.2.34. Здесь уровень собственных шумов (NPR) – это глубина режекции. Идеальный АЦП генерирует только шум квантования внутри полосы режекции, но на практике существуют дополнительные шумовые компоненты из-за интермодуляционных искажений, вызванных нелинейностью АЦП. Обратите внимание, что уровень собственных шумов достигает 60 дБ, тогда как расчетное значение равно 62,7 дБ.

ТЕОРЕТИЧЕСКИЙ УРОВЕНЬ ШУМА (NPR) ДЛЯ 10, 11 И 12-РАЗРЯДНЫХ АЦП

Рис. 2.33

12-РАЗРЯДНЫЙ 41 MSPS АЦП AD9042:

ИЗМЕРЕННЫЙ NPR 60 ДБ

(РАСЧЕТНОЕ ЗНАЧЕНИЕ 62,7ДБ)

Рис. 2.34

Дрожание апертуры и апертурная задержка

Другая причина того, что отношение сигнал/шум (SNR) АЦП уменьшается с увеличением входной частоты, может быть выведена из рис.2.35, который показывает эффекты дрожания фазы в дискретизаторе АЦП (или внутреннем в УВХ). Дрожание фазы вызывает ошибку напряжения, которая является функцией скорости нарастания сигнала и приводит к существенному ухудшению отношения сигнал/шум, как показано на рис.2.36. Это довольно серьезный эффект, особенно на высоких частотах входного сигнала. Поэтому, должна соблюдаться особая осторожность при минимизации фазового шума в дискретизаторах любой системы.

Эта осторожность должна распространяться на все компоненты, в которых присутствуют тактовые сигналы: непосредственно генератор (например, таймер серии 555 не отвечает требованиям, но даже кварцевый генератор может создавать проблемы, если он используется в активном устройстве совместно с шумной логикой); тракт передачи (эти тактовые сигналы очень уязвимы к помехам всех видов) и фазовый шум, вводимый в АЦП или ЦАП. Общим источником фазового шума в преобразователе является дрожание апертуры в общей цепи УВХ (SHA).

ВЛИЯНИЕ ДРОЖАНИЯ АПЕРТУРЫ

И ФАЗОВОГО ШУМА ТАКТОВОГО ГЕНЕРАТОРА

Рис. 2.35

Два десятилетия назад схемы дискретизации АЦП создавались отдельно из УВХ (SHA) и АЦП. Проектирование интерфейса было трудным делом, и главная причина этого заключалась в дрожании апертуры в УВХ. Сегодня большинство систем дискретизации использует схемы дискретизации АЦП с интегрированной схемой УВХ. Дрожание апертуры УВХ может быть не определено явным образом в спецификации, но это не служит поводом для беспокойства, если SNR или ENOB ясно определены. Иными словами, гарантия определенного отношения сигнал/шум (SNR) является неявной гарантией определенного адекватного значения дрожания апертуры. А использование дополнительной высококачественной схемы УВХ иногда приводит к улучшению значений эффективного числа разрядов (ENOB) на высоких частотах даже в лучших дискретизирующих АЦП и может оказаться более выгодным, чем замена АЦП на более дорогую модель.

Необходимо отметить, что существует также фиксированный компонент, который присутствует при определении апертуры дискретизации АЦП. Этот компонент, обычно называемый временем эффективной апертурной задержки, не дает ошибки. Его наличие приводит к появлению интервала между временем команды АЦП на дискретизацию и временем, когда получен реальный отсчет (см. рис.2.37). Интервал может быть положительным или отрицательным. Изменение или допуск этого параметра важны в приложениях с одновременной дискретизации с помощью двух АЦП или в других приложениях типа I- и Q-демодуляции, где два АЦП требуют совместной синхронизации.

УХУДШЕНИЕ SNR ИЗ-ЗА ДРОЖАНИЯ ФАЗЫ СИГНАЛА СИНХРОНИЗАЦИИ АЦП

Рис. 2.36

ВРЕМЯ ЭФФЕКТИВНОЙ АПЕРТУРНОЙ ЗАДЕРЖКИ

Рис. 2.37

Д ИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦАП

Очевидно, что для цифро- аналогового преобразователя наиболее важными являются такие характеристики сигнала, как время установки (settling time), всплеск сигнала вследствие перерегулирования при изменении сигнала на выходе ЦАП, называемый далее ложным сигналом (выбросом, glitch), искажения и свободный от помех динамический диапазон сигнала (SFDR).

Время установки ЦАП – это время от начала изменения цифрового кода до момента, когда сигнал стабилизируется в пределах некоторого диапазона ошибки, как это показано на рис.2.38. Сравнивать времена установки усилителей трудно, так как их диапазоны ошибки могут отличиться от усилителя к усилителю, но диапазон ошибки ЦАП практически не меняется и равен ±1 или ±½ LSB.

Время установки ЦАП состоит из четырех различных периодов: время переключения (в течение которого цифровое переключение осуществлено, но на выходе нет изменений), переходное время (slewing time) (в течение которого скорость изменения выходного сигнала ограничена скоростью нарастания на выходе ЦАП), время восстановления (recovery time) (когда ЦАП восстанавливает значение после быстрого перехода и может быть выброс на фронте) и линейное время установки (linear settling time) (когда значение на выходе ЦАП приближается к его конечной величине экспоненциально или почти экспоненциально). Если переходное время мало по сравнению с тремя другими (как это обычно бывает в случае с токовыми выходами ЦАП), то время установки не будет существенно зависеть от перепада уровня выходного сигнала. С другой стороны, если переходное время занимает существенную часть общего времени, то время установки будет тем больше, чем больше величина перепада.

ВРЕМЯ УСТАНОВЛЕНИЯ ЦАП

Рис. 2.38

В идеале изменения на выходе ЦАП от одной величины до другой должны проходить монотонно. На практике возможно появление выброса фронта (overshoot), отрицательного выброса перед фронтом (undershoot) или то и другое одновременно (см.

рис.2.39). Это неконтролируемое состояние выхода ЦАП в течение перехода известно как ложный сигнал. Он может являться результатом двух явлений: емкостной связи цифровых переходов с аналоговым выходом и свойствами некоторых ключей в ЦАП, работающих более быстро, чем другие, и создающих временные выбросы по уровню.

ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА ЦАП (С ПАРАЗИТНЫМИ ВЫБРОСАМИ)

Рис. 2.38

Емкостная связь часто дает примерно равные положительные и отрицательные выбросы (иногда называемые дуплетом ложного сигнала), которые далее в большей или меньшей степени удается компенсировать. Ложный сигнал, появляющийся вследствие несинхронности переключения, в общем случае униполярен, имеет большую амплитуду и представляет собой гораздо большую проблему.

Для оценки ложных сигналов измеряют площадь, огибаемую фронтом такого сигнала, и иногда неточно называемую энергией ложного сигнала. Употребление термина "энергия ложного сигнала" неправильно, так как площадь под кривой ложного сигнала измеряется вольт-секундами (Volt-seconds) (или более вероятно µV- секунды или pV- секунды). Пиковая площадь под кривой ложного сигнала – это площадь под максимальным положительным или отрицательным импульсом ложного сигнала. Площадь импульса ложного сигнала – это область под вольт-секундной кривой, которая может быть рассчитана после аппроксимации формы сигнала треугольниками и вычисления их площади посредством вычитания отрицательной площади из положительной. Величина ложного сигнала, порождаемого переходом между кодами 0111...111 и 1000...000, обычно является самой большой. Ложные сигналы в других точках перехода кода (таких как 1/4 и 3/4 полной шкалы) обычно имеют меньшую величину. На рис.2.40 отмечен ложный сигнал быстрого ЦАП с малым значением такого сигнала в середине его динамического диапазона. Пиковые и импульсные площади ложного сигнала рассчитываются с использованием треугольников, как это было описано выше. Время установки измеряется с момента, когда сигнал покидает начальный диапазон ошибки в 1 LSB, и до момента, когда он входит и остается в пределах конечного диапазона ошибки в 1 LSB.

Размер шага между областями перехода также равен 1 LSB.

ВЫБРОСЫ СИГНАЛА ЦАП:

СУММАРНАЯ ПЛОЩАДЬ ИМПУЛЬСА – 1.34 пВ·с

ВРЕМЯ УСТАНОВЛЕНИЯ – 4.5 нс

Рис. 2.40

Время установки ЦАП важно в таких приложениях, как блок развертки RGB-сигнала в мониторах, а характеристики в частотной области типа SFDR в общем случае более важны в телекоммуникациях.

Если мы рассмотрим спектр сигнала, преобразованного в ЦАП из цифровой формы, то обнаружим, что, в дополнение к ожидаемому спектру (который будет содержать одну или больше частот, в зависимости от природы восстановленного сигнала), в нем также будет присутствовать шум и составляющие искажений. Искажения могут быть определены в терминах нелинейных искажений, динамического диапазона, свободного от помех (SFDR), интермодуляционных искажений или всех вышеперечисленных вместе. Под нелинейными искажениями понимается отношение высших гармоник к гармонике основной частоты, на которой восстановлен чистый (теоретически) синусоидальный сигнал. Эти искажения являются наиболее общей характеристикой искажений. Динамический диапазон, свободный от помех (SFDR) – это отношение энергии наибольшей из гармоник (обычно – это гармоника основной частоты, но не обязательно) к энергии основной частоты.

При восстановлении с помощью ЦАП синусоидального сигнала, сгенерированного в системе прямого цифрового синтеза (DDS), зависимые от кода ложные сигналы формируют гармоники как внутри полосы, так и за ее пределами. Сигнал проходит через уровень, соответствующий середине шкалы, дважды за один цикл. Поэтому ложный сигнал имеет вторую синусоидальную гармонику, как показано на рис.2.41. Обратите внимание, что гармоники более высокого порядка, составляющие которых попадают в основную полосу Найквиста (от 0до fs /2), не фильтруются.

ПРОЯВЛЕНИЕ КОД-ЗАВИСИМЫХ ВЫБРОСОВ СИГНАЛА В СПЕКТРЕ ВЫХОДНОГО СИГНАЛА

Рис. 2.41

Руководствуясь одной лишь характеристикой площади под кривой ложного сигнала, трудно предсказать нелинейное искажение или SFDR. Другие факторы, такие как полная линейность ЦАП, также способствуют возникновению искажений.

Поэтому, общепринята проверка восстановительной способности ЦАП в частотной области (с использованием анализатора спектра) на различных тактовых и сигнальных частотах, как показано на рис.2.43. Типичное значение SFDR для 14-разрядного ЦАП AD9772 представлено на рис.2.44. Тактовая частота равна 65 MSPS и сигнальная частота анализируется до 25 MГц. Как и в случае с АЦП, шум квантования будет проявляться в виде увеличенного нелинейного искажения, если отношение между частотой синхронизации и выходной частотой ЦАП представляется целым числом. Таких отношений нужно избегать при измерении SFDR.

Разрешающая способность ЦАП

Общая нелинейность

Дифференциальная нелинейность

Код-зависимые выбросы

Отношение тактовой частоты к выходной (даже для идеального ЦАП)

Аналитический подход затруднен!

ИСТОЧНИКИ ИСКАЖЕНИЙ В ЦАП СИНТЕЗАТОРОВ ЧАСТОТЫ (DDS)

Рис. 2.42

СХЕМА ИЗМЕРЕНИЯ SFDR ЦИФРО-АНАЛОГОВОГО ПРЕОБРАЗОВАТЕЛЯ

Рис. 2.43

Спад частотной характеристики (Rolloff ) ЦАП sin (x)/x

Выходной сигнал ЦАП может быть представлен в виде ряда прямоугольных импульсов шириной, равной обратной величине тактовой частоты, как показано на рис.2.45. Обратите внимание, что восстановленная амплитуда сигнала составляет -3,92 дБ на частоте Найквиста fс /2. Для компенсации этого эффекта в большинстве случаев достаточно использовать инверсный фильтр sin(x)/x. Значения составляющих основной частоты также ослабляются функцией sin(x)/x.

СПЕКТР ВЫХОДОНОГО СИГНАЛА ЦАП С ОГИБАЮЩЕЙ ВИДА SIN X/X (АМПЛИТУДА НОРМАЛИЗОВАННАЯ)

Рис. 2.45

С ПИСОК ЛИТЕРАТУРЫ

Осокин Ю.В., Судьин С.Л., Федорков Б.Г "Параметры, области применения и перспективы развития полупроводниковых преобразователей информации// микроэлектроника и полупроводниковые приборы" под редакцией А.А. Васенкова и Я.А. Федотова. М.: Радио и связь. 1983.
Федорков Б.Г, Телец В.А. "Микросхемы ЦАП и АЦП: функционирование, параметры, применение" - М. Энергоатомиздат 1990.
W. R. Bennett, “Spectra of Quantized Signals”, Bell System Technical Journal, No. 27, July 1948, pp. 446-472.
Steve Ruscak and Larry Singer, Using Histogram Techniques to Measure A/D Converter Noise, Analog Dialogue , Vol. 29-2, 1995.
M.J.

Tant, The White Noise Book, Marconi Instruments, July 1974.
G.A. Gray and G.W. Zeoli, Quantization and Saturation Noise due to A/D Conversion, IEEE Trans. Aerospace and Electronic Systems, Jan. 1971, pp. 222-223.
Chuck Lane, A 10-bit 60MSPS Flash ADC, Proceedings of the 1989 Bipolar Circuits and Technology Meeting, IEEE Catalog No. 89CH2771-4, September 1989, pp. 44-47.
F.D. Waldhauer, Analog to Digital Converter, U.S. Patent 3-187-325, 1965.
J.O. Edson and H.H. Henning, Broadband Codecs for an Experimental 224Mb/s PCM Terminal, Bell System Technical Journal, 44, November 1965, pp. 1887-1940.
J.S. Mayo, Experimental 224Mb/s PCM Terminals, Bell System Technical Journal, 44, November 1965, pp. 1813-1941.
Hermann Schmid, Electronic Analog/Digital Conversions, Van Nostrand Reinhold Company, New York, 1970.
Carl Moreland, An 8-bit 150MSPS Serial ADC, 1995 ISSCC Digest of Technical Papers, Vol. 38, p. 272.
Roy Gosser and Frank Murden, A 12-bit 50MSPS Two-Stage A/D Converter, 1995 ISSCC Digest of Technical Papers , p. 278.
Carl Moreland, An Analog-to-Digital Converter Using Serial-Ripple Architecture, Masters' Thesis, Florida State University College of Engineering, Department of Electrical Engineering, 1995.
Walt Kester, Drive Circuitry is Critical to High-Speed Sampling ADCs, Electronic Design Special Analog Issue, Nov. 7, 1994, pp. 43-50.
Walt Kester, Basic Characteristics Distinguish Sampling A/D Converters, EDN, Sept. 3, 1992, pp. 135-144.
Walt Kester, Peripheral Circuits Can Make or Break Sampling ADC Systems, EDN , Oct. 1, 1992, pp. 97-105.
Walt Kester, Layout, Grounding, and Filtering Complete Sampling ADC System, EDN , Oct. 15, 1992, pp. 127-134.
Joey Doernberg, Hae-Seung Lee, David A. Hodges, Full Speed Testing of A/D Converters, IEEE Journal of Solid State Circuits, Vol. SC-19, No. 6, Dec. 1984, pp. 820-827.
Brendan Coleman, Pat Meehan, John Reidy and Pat Weeks, Coherent Sampling Helps When Specifying DSP A/D Converters, EDN, October 15, 1987, pp. 145-152.
James J.Colotti, Digital Dynamic Analysis of A/D Conversion Systems Through Evaluation Software Based on FFT/DFT Analysis, RF Expo East 1987 Proceedings, Cardiff Publishing Co., pp. 245-272.
Dan Sheingold, Editor, Analog-to-Digital Conversion Handbook, Third Edition, Prentice-Hall, 1986.
Lawrence Rabiner and Bernard Gold, Theory and Application of Digital Signal Processing, Prentice-Hall, 1975.
Matthew Mahoney, DSP-Based Testing of Analog and Mixed-Signal Circuits, IEEE Computer Society Press, Washington, D.C., 1987.
IEEE Trial-Use Standard for Digitizing Waveform Recorders, No. 1057-1988.
Richard J. Higgins, Digital Signal Processing in VSLI, Prentice-Hall, 1990.
Howard E. Hilton, A 10MHz Analog-to-Digital Converter with 110dB Linearity, H.P. Journal , October 1993, pp. 105-112.

Содержание раздела